Staircase design - basic

Using the requirements of Building Regulations Part K, and a known installation for a staircase, it is fairly straight forward to come up with the specification for a basic staircase for a domestic dwelling.

The starting point would be to measure the height between floor levels; in this example, the floor to ceiling height is 2.3m and the depth of the floor above is 0.3m, giving a total floor to floor measurement of 2.6m (2.6m is the standard floor to floor measurement in UK new build dwellings).

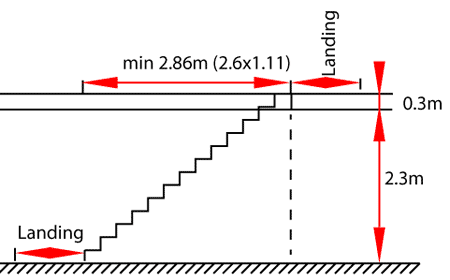
The maximum slope of the staircase is 42°, which means the horizontal measurement for the staircase must be a factor of 1.11 of the vertical measurement, which in this case comes to 2.86m.

(1.11 is achieved simply by using the tangent of 42° with a vertical measurement of 1, thus 1.11 can be used as a factor no matter what units of measurement are used. For a less steep staircase, 1.11 can be increased but should never be reduced.)

Assuming the stairs are to be 900mm wide, the clear landings at the top and bottom of the stairs must each be at least 900mm long, with no door opening closer than 400mm to either end of the staircase.

The individual risers must be between 150 and 220mm, so to achieve the total vertical measurement of 2.6m, the number of risers must be between 17 and 12 - with each riser between 153 and 217mm.

The individual goings must be between 220 and 300mm, so to achieve a total horizontal distance of 2.86m, the number of goings must be between 12 and 10 - with each going between 238 and 286mm.

As there must be as many risers as goings in a staircase, the only option at this stage in this example is for 12 risers each 217mm, and 12 goings each 238mm. Using the "going plus two risers" rule, this gives 672mm - which is acceptable.

The floor to floor measurement is fixed by the building, so any adjust will have to be by increasing the horizontal distance (which will reduce the pitch angle).

For an even shallower staircase, the goings could be any size up to 300mm (2x217 + 266 = 700mm) - with 266mm goings, the horizontal floor space with 12 goings would be 3.192m.

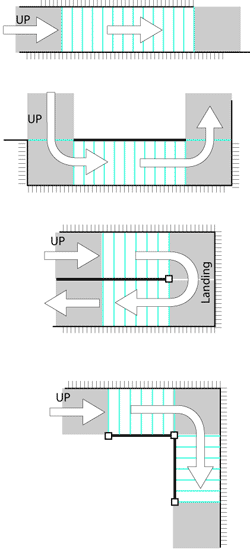
If there is not enough floor space for a straight staircase, it might be possible to rearranged the stairs so that it makes one or more turns while keeping the same number of risers. Each turn would usually require a landing which would take up additional floor space, but overall the stairs might fit better into the situation. Below are 4 examples of how the same number of risers can be rearranged to offer different overall plan shapes (the turquoise lines indicating individual risers, the grey areas being the required landings).

Spiral Staircases

Spiral Staircases need to meet the requirements of the Building Regulations Part K and details of design are covered in BS 5395-2.

For domestic dwellings Spiral Staircases are typically between 1.8 and 2.25m overall diameter. Smaller Spiral Staircases, 1.3 to 1.8m in diameter, may be used in limited circumstances.